Уравнение регрессии
Уравнение регрессии
Уравнение, описывающее обычную взаимосвязь между зависимой переменной и набором казуальных переменных.
Регрессии уравнение
уравнение линии, вокруг которой группируются точки корреляционного поля; указывает основное направление и тенденцию связи.
Источник: Глоссарий по эконометрике. Проект ru.wikiversity.org
УРАВНЕНИЕ РЕГРЕССИИ
(корреляции), уравнение, определяющее «форму связи» между статистич. признаками, а именно зависимость средней величины одного признака от значения, принимаемого другим. У. р. может быть выражено различными математич. функциями: прямой, кривыми 2-го, 3-го, 4-го и т. д. порядков, гиперболой, показательной функцией и др. Важной проблемой является выбор типа функции уравнения, при к-ром исходят гл. обр. из анализа природы данных факторов и их связи. Это не исключает учёта и эмпирич. поведения средней величины зависимого признака при разных значениях признака-аргумента. Дальнейший поиск У. р. состоит в нахождении его параметров. В большинстве случаев при этом исходят из принципа наиболее полного совпадения У. р. с описываемой им связью, т. е. наибольшего приближения значений, вычисленных по У. р., к фактич. значениям признака. Распространённый способ достижения этого — способ наименьших квадратов, по к-рому сумма квадратов отклонений фактич. данных от найденных по уравнению была бы минимальной. Это условие применительно к линейному уравнению парной регрессии у = а0 + а1х (где х и у — признаки) приводит к системе т. н. нормальных уравнений:
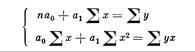
(п — число плюющихся пар значений х и у). Из них и определяются параметры уравнения. При параболич. У. р. 2-го порядка у = а0 + а1х + а2х2 система уравнений принимает вид:

При построении линейного множественного У. р. по признакам х1 х2 х3,... оно приобретает вид: у = а0 + + а1х1 + а2х2 + а3х3 + ... Система нормальных уравнений способа наименьших квадратов при двух факторах х1 и х2 будет такой:
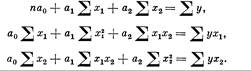
У.р. строится и в стандартизованном масштабе, когда вместо каждой переменной берётся стандартизованная величина, представляющая собой отношение отклонений её фактич. значения от средней к среднему квадратическому отклонению, т. е. х1 заменяется на
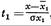
на
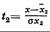
и т.д. а у на
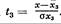
. При выборе признаков-аргументов (факторов) для построения У. р. статистикой выработаны нек-рые условия, позволяющие более правильно пользоваться им. У. р. тем точнее отображает связь между явлениями, чем на большем числе наблюдений оно построено. Факторные признаки, включаемые в уравнение, должны быть логически связаны с исследуемым «результативным» признаком.
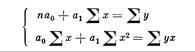
(п — число плюющихся пар значений х и у). Из них и определяются параметры уравнения. При параболич. У. р. 2-го порядка у = а0 + а1х + а2х2 система уравнений принимает вид:

При построении линейного множественного У. р. по признакам х1 х2 х3,... оно приобретает вид: у = а0 + + а1х1 + а2х2 + а3х3 + ... Система нормальных уравнений способа наименьших квадратов при двух факторах х1 и х2 будет такой:
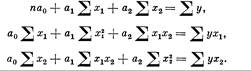
У.р. строится и в стандартизованном масштабе, когда вместо каждой переменной берётся стандартизованная величина, представляющая собой отношение отклонений её фактич. значения от средней к среднему квадратическому отклонению, т. е. х1 заменяется на
на
и т.д. а у на
. При выборе признаков-аргументов (факторов) для построения У. р. статистикой выработаны нек-рые условия, позволяющие более правильно пользоваться им. У. р. тем точнее отображает связь между явлениями, чем на большем числе наблюдений оно построено. Факторные признаки, включаемые в уравнение, должны быть логически связаны с исследуемым «результативным» признаком.
Источник: Экономическая энциклопедия. Политическая экономия в 4 т. Советская энциклопедия 1979-1980 гг.





