СИСТЕМА ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

совокупность экономико-математических моделей, объединённых объектом моделирования или общей целью так, что результаты расчётов по одним моделям являются исходной информацией для других. Модели образуют систему при условии их внутренней согласованности и наличии средств сопряжения. Различают декомпозиционный и синтетич. подходы при построении С.э.-м.м. При декомпозиционном подходе исходной принимается единая общая модель, к-рая затем разбивается на блоки или подмодели. Каждый блок обособляется, разрабатывается и развивается в какой-то степени независимо, иногда отд. коллективом. При синтетич. подходе исходными являются отд. экономико-математич. модели. Они объединяются в систему с помощью разработки спец. требований и стандартов к содержанию и структуре входных и выходных массивов информации, правил взаимодействия и совместного функционирования. Общая цель системы при этом синтезируется из частных целей объединяемых моделей. С.э.-м.м. характеризуют качественно более высокий уровень экономико-математич. моделирования по сравнению с разработкой и использованием отд. моделей. Они более адекватны экономич. действительности. Отд. модель, как правило, не охватывает разные виды деятельности, характеризуется единообразием применяемого математич. аппарата, ориентирована на использование в одном н.-и., плановом или управляющем органе. Отд. модель труднее использовать в практике планирования и управления, т. к. она не сопрягается органически с действующими методами. Попытки встроить отд. модель в реальный механизм управления приводят к необходимости создания системы. С.э.-м.м. благодаря т. и. эффекту системности несёт в себе новые качества по сравнению с отд. моделью.
Разрабатываемые С.э.-м.м. охватывают весь спектр процессов, происходящих в экономике, на любых её уровнях. Рассмотрим С.э.-м.м. для отд. процессов - процесса планирования, с целью её самостоятельного использования и последующего включения в более общую систему. Упрощённый вариант С.э.-м.м. нар.хоз. планирования см. на рис. 1.

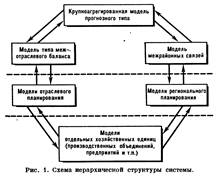
На схеме стрелками указаны информационные потоки; пунктирной линией отделены уровни планирования: высший (Сов. Мин. СССР, Госплан СССР), средний (союзные и союзно-респ. мин-ва и ведомства, территориальные органы планирования и управления) и нижний (пром. и производств. объединения, предприятия). Каждая модель, приведённая на схеме, представляет целый комплекс взаимоувязанных моделей, то есть С.э.-м.м. Причём этот комплекс в известной степени повторяет структуру всей системы. Особенно это относится к подсистеме высшего уровня планирования, к-рую в данном изложении можно представлять себе точной копией (в структурном отношении) всей системы.
Подобная С. э.-м. м. - необходимый этап в применении ЭВМ при разработке нар.-хоз. планов. Дальнейшее повышение уровня сбалансированности, комплексности, оптимальности планов невозможно без использования современных экономико-математических и технических средств.
С.э.-м.м. - теоретич. основа автоматизированных систем управления (АСУ), и в первую очередь это относится к системам моделей планирования. Разрабатываемая в СССР автоматизированная система плановых расчётов (АСПР) для Госплана СССР и Госпланов союзных республик базируется на комплексе экономико-математич. моделей описываемого типа. Аналогичным образом стержнем отраслевых автоматизированных систем управления является С.э.-м.м. отраслевого планирования (см. рис. 2).

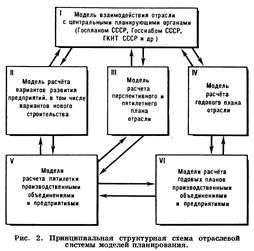
На рис. 2 модели I, III и IV - инструмент планирования в самом мин-ве, модель II разрабатывается и функционирует в головном проектном ин-те отрасли, модели V и VI, соответственно, в производств. объединениях или на предприятиях. Схема указывает на потоки передаваемой информации между различными уровнями планирования и управления и порядок их взаимодействия.
Системы моделей планирования являются наиболее разработанными С.э.-м.м. Дальнейшим их развитием служат системы, моделирующие не только процесс планирования, но и процесс произ-ва (процесс выполнения плана), управление и контроль за выполнением плана, финанс. деятельность, сбыт, материально-технич. снабжение, процесс подготовки произ-ва, создания и внедрения в произ-во новшеств, потребление продукции и услуг населением. Моделирование этих процессов и видов деятельности во многом использует аппарат имитации, проигрывания ситуаций на ЭВМ, методы математической статистики, корреляционный анализ (см. Корреляция), планирование эксперимента и др.; требует разработки новых средств экономико-математического описания, формализации, новых форм и режимов практич. использования моделей. Поэтому такие системы моделей носят комплексный характер, состоят из разнородных по применяемому математическому аппарату блоков. Например, модели планирования базируются в основном на аппарате линейной алгебры и математического программирования (линейное, выпуклое, целочисленное программирование). Модели процессов согласования плановых и др. решений различных уровней, в частности процессов согласования целевых функций, используют аппарат векторной оптимизации, теории игр, моделей экономич. равновесия, теории принятия групповых решений (модели голосования, экспертные оценки и т. д.).
Объединение разнородных моделей в систему требует тщательной проработки вопросов их стыковки, согласования решений, вариантов режимов использования. Это качественно новый вид деятельности, в рамках к-рого ведутся интенсивные науч. исследования. Прежде всего это проблема согласования решений моделей, входящих в систему. Рассмотрим двухуровневую систему моделей планирования, в к-рой на верхнем уровне - модель межотраслевого баланса, а на нижнем - оптимизационные модели отраслей. В модели межотраслевого баланса определяются объёмы выпуска продукции отраслей

, удовлетворяющие балансовым соотношениям X = АХ + Z, где А - матрица коэффициентов текущих затрат, Z - вектор объёмов конечного продукта (конечное потребление и капиталовложения). Для каждой отрасли i (i = 1, ..., n) определяется вектор объёмов использования производств. способов
из условий:


(Критерий оптимальности - минимум затрат, напр. трудовых).
Верхний уровень передаёт нижнему задания по выпуску продукции. Каждая отрасль в результате решения своей задачи определяет потребность в продукции всех др. отраслей:

, столбцы матрицы Вi указывают затраты продуктов отраслей при единичной интенсивности применения производств. способов (использования фондов) отрасли. Свои потребности отрасли передают наверх. На основании полученной информации строится матрица А. А именно столбец Ai матрицы А есть

. Планы верхнего и нижнего уровней

следует считать согласованными в том случае, когда соответств. передача информации из одного уровня на другой не меняет решения.
Согласованные решения, как правило, определяются неоднозначно, особенно в системах с неск. уровнями. Свойства множеств согласованных решений поддаются анализу в рамках теории игр.
Другая важная проблема, тесно связанная с согласованием решений, - формирование и согласование целей (критериев оптимальности) различных уровней. При декомпозиционном подходе к построению С. э.-м. м., используемом гл. обр. для разработки моделей планирования, общая цель для всей системы задана, а целевые функции составных частей формируются исходя из этой общей цели. Методика декомпозиции целей хорошо разработана для моделей оптимального планирования, базирующихся на методах блочного программирования. При синтетич. подходе, более универсальном и реалистичном, целевые функции частей (напр., групп населения) являются исходными, заданными. Задача состоит в определении такого взаимодействия частей внутри системы и такого порядка функционирования, при к-ром вся система в целом достигла бы решения, соответствующего глобальной цели. Проблемы синтеза общей цели на основе частных ставятся и решаются в теории игр, моделях векторной оптимизации, моделях экономич. равновесия, теории принятия групповых решений, а также методами имитационного моделирования. В имитационных моделях, понимаемых достаточно широко, переменными или варьируемыми параметрами могут выступать алгоритмы принятия решений отд. подмоделями, а также алгоритмы согласования решений. Следовательно, задача состоит в нахождении такого набора алгоритмов, имитирующих функционирование экономич. системы, при к-ром получаемое общее решение наилучшим образом соответствует глобальной цели системы.
При построении и особенно практич. использовании С. э.-м. м. важную роль играет «человеческий фактор». Чем сложнее система моделей, тем больше остаётся неформализованных процедур, к-рые осуществляет человек. Аппаратом исследования взаимодействия человека и формализованных моделей являются деловые игры, хорошо зарекомендовавшие себя, как способ получения согласованных решений при наличии неформализованной ситуации.
При разработке С.э.-м.м. и внедрении их в практику планирования и управления нар. х-вом возникает ряд специфич. проблем организационного, математич. и технич. порядка (информационное, математич. и технич. обеспечение). Создание гибкого, достаточно полного банка данных, содержащего постоянно пополняемую и обновляемую достоверную информацию, - сложная в социально-организац. и технич. плане задача. Математич., в т. ч. программное, обеспечение для С.э.-м.м. разрабатывается многочисл. коллективами, ориентируясь как на отд. типы ЭВМ, так и на системы ЭВМ.
С. э.-м. м. являются теоретич. основой и ядром в создаваемых и уже функционирующих АСУ. Особенно это относится к автоматизированной системе плановых расчётов (АСПР) и отраслевым автоматизированным системам управления (ОАСУ). Создание единой общегос. системы сбора и обработки информации (ОГАС) невозможно без предварит, проработки С. э.-м. м., лежащей в основе ОГАС. Работы в этом направлении проводятся в СССР ведущими н.-и. учреждениями в области планирования и управления (Центр. экономико-математич. ин-т АН СССР, Ин-т экономики АН СССР, НИЭИ Госплана СССР, Ин-т планирования и управления АН СССР, Ин-т экономики и организации пром. произ-ва Сиб. отделения АН СССР, вычислит. центр АН СССР, ВНИИ проблем организации и управления Гос. к-та СССР по науке и технике и др.).
Системный подход к проблемам планирования и управления нар. х-вом, базирующийся в значит. мере на С. э.-м. м., оказывается плодотворным также в анализе нек-рых теоретич. проблем экономич. науки. Принятые 25-м съездом КПСС положения о планировании и оценке результатов экономич. деятельности по конечным целям конкретизируют направления использования системного подхода применительно к проблемам экономики развитого социалистич. общества.