Моделирование Экономических Процессов Математическое

выражение на математич. языке основных свойств, сторон экономич. процессов в их взаимной связи и обусловленности. Математич. модель любого явления в природе и обществе представляет собой его научное обобщённое отражение, существенным моментом к-рого является выявление количественных характеристик, присущих изучаемому явлению. Построение математич. модели процесса (объекта) - высокая ступень его научного анализа.
Модель процесса, в т. ч. и экономическая, может быть сформулирована при помощи самого разнообразного языка. Могут быть построены словесная, графич., физич., математич. и др. модели объекта. Модель должна строиться на том языке, который наиболее развит, точен, имеет гибкую систему понятий, позволяющую в максимальной степени адекватно описывать сложные взаимосвязи изучаемого объекта, располагает аппаратом, способным их анализировать. Таким наиболее универсальным языком, позволяющим проводить качественный и количественный анализ экономич. процессов в органическом единстве, является математик, язык. М. м. э. и. позволяет глубже вскрыть их внутреннюю сущность, механизм развития, такие черты, к-рые были неизвестны до моделирования.
Наиболее часто математик, модель экономик, процесса представляет собой систему уравнений и неравенств, состоящих из набора переменных величин и параметров. Переменные математик, модели характеризуют определённые экономик, величины (напр., объём выпускаемой продукции, объём капитальных вложений в нар. х-ве и т. п.), а параметры - количественные связи между отдельными экономик, величинами (напр., нормы расхода металла на произ-во станков определённого типа и т. п.). Переменные, значения к-рых в модели являются определёнными, наз. экзогенными, автономными. Переменные, значения к-рых должны быть найдены в результате анализа системы уравнений, образующих математик, модель экономик, процесса, - эндогенными. Количественное решение математик, модели экономик, процесса предполагает нахождение значений неизвестных (эндогенных) переменных величин, к-рые должны быть выражены через значение параметров и известных (экзогенных) переменных или должен быть дан алгорифм их нахождения по этим данным.
Математич. моделирование изучаемого экономич. процесса начинается с выделения его наиболее существенных свойств и сторон, описания их количественных взаимозависимостей. Математик. модель, являясь научной абстракцией экономик, процесса, должна отражать, отвлекаясь от второстепенных, только главные, важнейшие его характеристики, закономерности развития, определяющие его внутреннюю природу, т. к. в противном случае математик, модель становится чрезвычайно громоздкой и не поддаётся анализу. При этом в зависимости от цели научного анализа разрабатывают математик, модель или объекта в целом, или его части, или моделируют лишь определённые его функции. Усложнять модель необходимо только в том случае, если это может привести к получению новых существенных выводов о природе объекта или уточнению его характеристики. С др. стороны, построение излишне упрощённой модели объекта может привести к тому, что она не будет адекватной моделируемому объекту, и полученные на её основе выводы потеряют практическую и познавательную ценность. Т. о. границы сложности математик, модели определяются, с одной стороны, необходимостью адекватности, а с другой - возможностями математич. аппарата и вычислительной техники, а также информационного обеспечения.
Математич. моделирование определённого экономик, процесса принципиально может выполнять две функции: отражать существующий экономич. процесс; определять желательное (планируемое) протекание экономик. процесса. В первом случае математик, модель описывает реально существующий экономик, процесс, взаимосвязь включённых в него экономик, величин-переменных и параметров с целью выявить объективно существующие основные свойства процесса, его природу. Во втором - математик, модель играет активную роль; она должна показать как будет или как должен протекать экономик, процесс, если в его основу положить определённую систему конституирующих его природу предпосылок. Центр тяжести математик, моделирования здесь переносится на то, чтобы была правильно сформулирована система предпосылок, к-рая должна определить желательную природу планируемого экономик. процесса. Так, до проведения в СССР экономик, реформы (1966) пром. предприятия функционировали в определённых условиях, на основе данной системы предпосылок (показателей), к-рые характеризовали способ их хозяйствования. Математик, модель экономик. деятельности предприятия в этом случае отражала бы его функционирование при данных экономик, условиях. Напротив, математик, модель экономик, деятельности предприятия, построенная на основе тех принципов хозяйствования, к-рые вытекают из экономик, реформы, показала бы как будет функционировать предприятие в новых условиях. Меняя на основе экономик, соображений систему показателей, к-рые должны составлять фундамент хоз. деятельности предприятия, при помощи математик, моделирования можно анализировать различные варианты протекания экономик, процессов и выбирать из них наиболее желательный. В реальной действительности обе эти функции математик. моделирования находятся в органическом единстве. Для того чтобы изменять характер протекания экономич. процесса, необходим тщательный анализ его существующего состояния, выяснение качественной и количественной взаимозависимости его осн. элементов. Только на этой основе планирование экономик, процесса, инструментом к-рого является математич. моделирование, может привести к хорошим результатам. В планомерно развивающейся социалистич. экономике осн. внимание должно уделяться активной функции математик, моделирования, призванного конструировать новые формы функционирования экономических объектов.
В М. м. э. п. условно можно выделить два этапа: создание математик, модели процесса, выраженной на языке математик, символов; заполнение модели конкретными числовыми значениями переменных и параметров. Оба этапа одинаково важны с точки зрения того, чтобы математик, модель в необходимой степени адекватно отражала моделируемый экономик, процесс. На первом этапе определяются важнейшие свойства и черты изучаемого процесса, а также принципиальные функциональные зависимости между входящими в него переменными величинами, на втором - числовые значения переменных и параметров. Как бы точно математик, модель ни отражала изучаемый экономик, процесс, полученные на её основе выводы не смогут иметь практик. ценности, если будут неправильно определены числовые значения параметров и экзогенных переменных модели. Необходимость адекватности модели изучаемому экономик, объекту, а также возможность получения соответствующей экономик, информации о параметрах и переменных математик, модели и возможности электронной вычислит. техники в решающей степени определяют размерность математик, модели экономик. процесса данного типа, т. е. количество составляющих её уравнений и переменных.
В зависимости от целей и задач, к-рые решаются М. м. э. и., модели в известной мере условно можно разделить на статические и динамические. В статич. моделях все экономик, показатели привязываются к определённому моменту времени и не рассматривается связь между показателями разных периодов развития экономик, объекта. В динамик, моделях развитие экономик, процесса рассматривается во времени (т. е. рассматривается временная взаимосвязь экономик. показателей).
Модели могут различаться по уровню исследуемого экономик, объекта. Напр., могут быть построены математик, модели функционирования отдельного цеха, предприятия, производств. объединения, отрасли, экономик, р-ыа, экономики союзной республики, нар. х-ва страны в целом. В этом случае природа экономик, объекта моделирования определяет специфику построения соответствующей математик, модели. Напр., экономик, величины, являющиеся экзогенными, заданными вне модели переменными, в математик. модели хоз. деятельности предприятия обычно являются эндогенными переменными в математик, модели отрасли и т. д. Уровень, который занимает модулируемый объект в иерархии, структуре планирования и управления экономикой, определяет характер описания ограничений модели (наличные производств. мощности, трудовые ресурсы, запасы сырья, материалов и т. п.), экономич. выбора и математич. формулировки критерия оптимальности функционирования хоз. объекта, источники и методы получения соответствующей экономич. информации, к-рая наполняет математич. модель, степень агрегирования её и т. д. Как показывает опыт, наибольшее применение в планировании и управлении получили математич. модели экономич. объектов, относительно более низких ступеней нар.-хоз. иерархии - предприятия и отрасли. Это прежде всего потому, что на этом уровне более просто, по сравнению с нар. х-вом страны в целом, формулируется критерий оптимальности хоз. деятельности объекта, меньше объём необходимой экономич. информации и она более доступна. В то же время эффективность М. м. э. п. более низких нар.-хоз. уровней значительно возрастает, если они рассматриваются как органические элементы математич. модели функционирования социалистич. экономики в целом. Это одна из причин необходимости сосредоточения научных исследований прежде всего на построении математич. модели оптимального функционирования социалистич. экономики в целом.
По природе функциональных проблем экономико-математич. модели делятся на балансовые модели и модели оптимального функционирования экономич. объектов. И те и другие могут быть построены для экономич. объектов любого уровня нар.-хоз. иерархии. Балансовые модели экономич. объектов с математич. точки зрения характеризуются единственностью решения. С экономич. точки зрения это означает, что с помощью математич. балансовых моделей при заданных параметрах и выбранных значениях экзогенных переменных можно составить только один вариант плана функционирования экономич. объекта, в к-ром устанавливаются необходимые пропорции между его отд. элементами. Балансовые модели не решают проблему выбора наилучшего варианта плана функционирования экономич. объекта. Математич. модели оптимального функционирования позволяют из множества вариантов плана выбрать такой, в к-ром с точки зрения принятого критерия оптимальности ресурсы используются наилучшим образом. Математически решение задачи оптимального функционирования экономич. объекта означает нахождение условного экстремума (максимума или минимума) нек-рого функционала, который рассматривается как критерий оптимальности (целевая функция) деятельности экономич. объекта. Математич. модели оптимального функционирования одновременно решают (включают в себя как частный случай) и проблемы математич. балансовых моделей. Модели оптимального функционирования экономич. объектов органически сочетают в себе методы установления пропорциональных планов с выбором наиболее эффективных планово-экономич. решений. Поэтому эти модели - наиболее адекватное отражение экономич. процессов в условиях социализма.
По виду функциональной зависимости между переменными, входящими в систему уравнений модели, их делят на линейные и нелинейные. Большинство функциональных зависимостей между экономич. переменными имеет нелинейный характер. Однако при решении задач на основе нелинейных моделей сложно получить соответствующую экономич. информацию и они труднее поддаются математич. обработке. Поэтому часто приходится апроксимировать нелинейные связи между переменными их линейными приближёнными. Кроме того, как показывает опыт, для решения задач можно использовать линейные функциональные зависимости между экономич. переменными.
Математич. модели можно разделить на однопродуктовые и многопродуктовые. При построении однопродуктовых моделей предполагается, что в нар. х-ве производится только один продукт, за счёт к-рого осуществляется возмещение и накопление средств произ-ва и потребление. Другими словами, предполагается, что продукт эластично может быть превращён в натуральную форму любых средств произ-ва и предметов потребления. Однопродуктовые модели обычно используются на «предварительной стадии» разработки плана развития нар. х-ва, когда определяются его самые общие контуры.
При построении многопродуктовых моделей предполагается, что производятся несколько продуктов, выполняющих различную экономич. роль в процессе общественного воспроизводства. Многопродуктовые модели строятся на основе однопродуктовых и применяются при разработке развёрнутого плана развития нар. х-ва.
Математич. модели могут быть краткосрочного (квартал, год), среднесрочного (до 5 лет), долгосрочного (до 15 лет) планирования и долгосрочного прогнозирования (до 20 лет) развития определённого экономич. объекта (напр., отрасли нар. х-ва в целом). В зависимости от длительности планового периода могут меняться ограничения моделей, их размерность, методы формирования планово-экономич. информации о параметрах и экзогенных переменных модели и т. д.
Наконец, важным является разделение экономико-математич. моделей на модели, к-рые изучают объект одного уровня нар.-хоз. иерархии (модели с простой структурой), и модели, к-рые исследуют взаимосвязи объектов разных уровней нар.-хоз. иерархии (модели со сложной структурой). Поскольку в реальной действительности функционирование нар. х-ва есть взаимодействие экономич. объектов, находящихся на разном уровне хоз. иерархии, последний класс моделей является наиболее адекватным способом отражения экономич. жизни социалистич. общества.
Кроме того, в зависимости от предположения относительно характера изменения параметров и экзогенных переменных в будущем математич. модели экономич. процессов делятся на модели детерминированного и вероятностного, стохастического типа. В последнем случае значения параметров и переменных заменяются их математич. ожиданиями.
В качестве примера ниже приводятся две математич. модели общественного произ-ва, к-рые иллюстрируют в общих чертах проблемы М. м. э. п.
1. Математическая модель межотраслевого баланса производства и распределения продукции в нар. х-ве (балансовая модель) основана на предположении, что каждый продукт производится одним технология. способом и в каждой отрасли производится один продукт. Эта модель позволяет получить единственный вариант плана. Она не содержит ограничений на ресурсы и не включает в себя критерия оптимальности плана. Модель строится след. образом.
Распределение продукции в нар. х-ве можно охарактеризовать след. системой балансовых соотношений:

где Хi - объём валовой продукции отрасли i; Xij- объём продукции отрасли i, идущей в текущее производственное потребление в отрасль

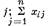
- объём промежуточной продукции отрасли i; Yi - объём конечной продукции отрасли i.
Первое предположение, из к-рого исходит рассматриваемая модель, - вся продукция делится на промежуточную и конечную.
Предположив далее, что

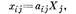
где Aij - коэффициенты затрат продукции отрасли г на единицу продукции отрасли i, получим систему уравнений статической математич. модели межотраслевого баланса:

2. Математическая модель оптимального планирования общественного производства, в простейшей форме формулируется след. образом. Требуется, чтобы

достигал максимального (минимального) значения. В данном случае в качестве критерия оптимальности может быть выбрана, напр., максимизация уровня жизни населения, т. е. коэффициенты Cj будут показывать, какое влияние на повышение уровня жизни оказывает выпуск единицы продукта j. Рассматриваемая модель позволяет составить не просто сбалансированный, но и оптимальный с точки зрения выбранного критерия вариант плана развития общественного произ-ва. Решается эта модель методами линейного программирования (см. Математические методы в экономических исследованиях).